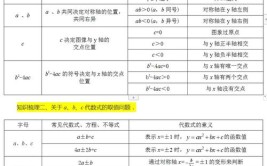
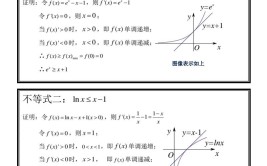
表现形式不同:
函数连续是此函数的图像是连续的曲线,没有间断点。
导函数连续是此函数的图像是光滑的,没有尖点。
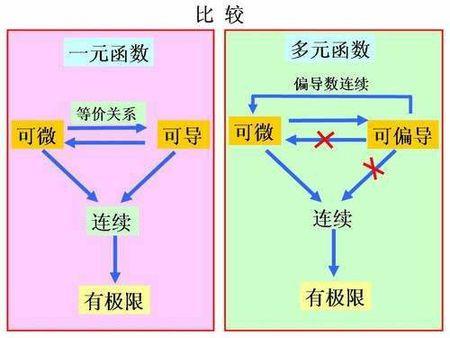
(图片来自网络侵删)
函数在该处的极限等于函数在该处的取值
相关介绍关系不同:
可导,导数不一定连续
导数连续,函数一定可导
连续不一定可导,比如函数Y=│X│在X=0处连续,但不可导;
但一个函数要想在一个点处可导,就必须要在此处连续。
应用不同:
连续函数的导函数不一定连续 f(x)=x^2*sin(1/x),(x≠0时),f(0)=0.
f′(x)=2x*sin(1/x)-cos(1/x),(x≠0时),f′(0)=0.
f′(x)在x=0不连续。