土木吧

金波，一级注册结构工程师，教授级高级工程师。
已出版《高层钢结构设计计算算例》、《钢结构设计及计算实例-基于<钢结构设计标准>GB 50017-2017》。
本文摘自作者即将出版的《建筑结构设计疑难问题剖析》一书。

《建筑地基基础设计规范》GB 50007-2011第1.0.1条的条文说明指出，由于地基土的变形具有长期的时间效应，与钢、混凝土、砖石等材料相比，它属于大变形材料。
从已有的大量地基事故分析，绝大多数事故皆由地基变形过大或不均匀造成。

《建筑地基基础设计规范》GB 50007-2011中，地基承载力计算pk≤fa、pkmax≤1.2fa不是强制性条文、而地基变形允许值是强制性条文。

因此计算地基变形、基础沉降非常重要，甚至比地基承载力计算更为重要。
地基变形计算主要有以下几种方法：

1.《建筑地基基础设计规范》GB 50007-2011第5.3.5条天然基础

计算地基变形时，地基内的应力分布，可采用各向同性均质线性变形体理论。
其最终变形量可按下式进行计算（图1）

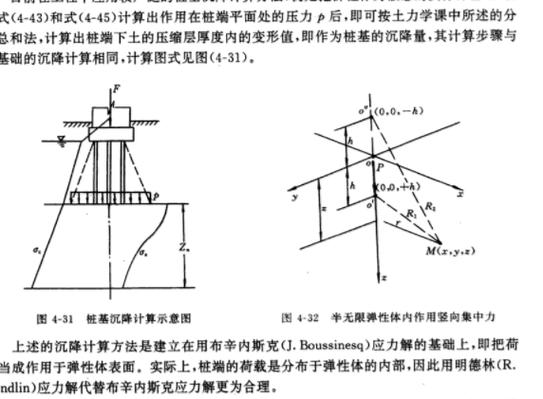
图1 基础沉降计算的分层示意

1885年，法国数学家布辛奈斯克（Joseph Valentin Boussinesq，1842～1929)用弹性理论推导出了在半无限空间弹性体表面上作用有竖向集中力P时，在弹性体内任意点M所引起的应力解析解。
以集中力P的作用点为原点，M点坐标为（x，y，z），如下图2所示，点M’为点M在弹性体表面的投影。
由布辛奈斯克得到的M点的6个应力分量和3个位移分量，其中对地基变形计算意义最大的是竖直法向正应力[2]：

图2 集中荷载作用下的应力（布辛奈斯克解）

布辛奈斯克是法国著名物理学家和数学家。
1842年3月13日生于法国Saint-Andre- de-Sangonis，1929年2月19日卒于巴黎。
1876年获得博士学位后，先后在多所学校担任数学教师，之后担任里尔理学院(Faculty of Sciences of Lille)的微积分教授、(Sorbonne)巴黎大学数学和物理系教授，1886年当选法国科学院院士。
1886年至1918年退休前任巴黎科学院的力学教授。
布辛尼斯克一生对数学物理中的所有分支（除电磁学）都有重要的贡献。
在流体力学方面，他主要研究涡流、波动、固体物对液体流动的阻力、粉状介质的力学机理、流动液体的冷却方面。
在紊流方面的成就深得著名科学家圣维南(Saint Venant)的赞赏，而在弹性理论方面也有突出贡献，如土力学中附加应力的布辛奈斯克解。
对数学，尽管他的初衷是用其解决实际问题，但依旧做出了突出的贡献。

2.《建筑地基基础设计规范》GB 50007-2011桩基础

《建筑地基基础设计规范》GB 50007-2011第8.5.15条规定，计算桩基沉降时，最终沉降量宜按单向压缩分层总和法计算。
地基内的应力分布宜采用各向同性均质线性变形体理论，按实体深基础方法或明德林应力公式方法进行计算，计算按《建筑地基基础设计规范》GB 50007-2011附录R进行。

《建筑地基基础设计规范》GB 50007-2011第R.0.1条规定，桩基础最终沉降量的计算采用单向压缩分层总和法：

（1）实体深基础方法

《建筑地基基础设计规范》GB 50007-2011第R.0.2条规定，采用实体深基础计算桩基础最终沉降量时，采用单向压缩分层总和法按《建筑地基基础设计规范》GB 50007-2011第5.3.5条～第5.3.8条的有关公式计算，也就是公式（1）。

《建筑地基基础设计规范》GB 50007-2011第R.0.2条规定，公式（1）中附加压力计算，应为桩底平面处的附加压力。
实体基础的支承面积可按图3采用。
实体深基础桩基沉降计算经验系数ψps应根据地区桩基础沉降观测资料及经验统计确定。
在不具备条件时，ψps值可按表1选用。

（a） （b）

图3 实体深基础的底面积

实体深基础计算桩基沉降经验系数 表1

很显然，《建筑地基基础设计规范》GB 50007-2011桩基沉降计算的实体深基础方法仍为布辛奈斯克解的沉降计算方法。
实体深基础方法基于以下两个假定：作用于土体的荷载都集中在桩尖平面上；以桩尖平面作为半无限体的表面，桩尖以上的土体的影响以及这部分土体与桩的相互作用都忽略不计。
实体深基础假定实际并没有深基础，它将桩尖平面以上所有的东西都抛掉了，把桩群抛掉了，把基础抛掉了，将桩尖平面看成是弹性半无限体的表面，使我们就可以像计算天然基础的沉降一样，用布辛奈斯克解计算桩基础的沉降。
显然实体深基础方法的假定很牵强，因此有人想用种种扩散角的办法来扩大桩尖平面的受荷面积、也就是将荷载沿桩群外侧扩散，以达到将上部附加荷载施加到桩尖平面的目的，使之更符合实际。
但是这种应力扩散方式也只是一种人为的猜想，没有理论或实验验证[1]。

因此，如果桩较短，桩侧土性质差，则实体深基础方法的假定和实际情况比较接近；但是如果桩长、桩侧土好，则实体深基础方法的假定和实际情况出入就大，桩越长、桩侧土越好，计算结果和实际差异就大，也就是计算结果大于实际结果[3]。

（2）明德林应力公式方法

《建筑地基基础设计规范》GB 50007-2011第R.0.4条规定，采用明德林应力公式方法进行桩基础沉降计算时，单向压缩分层总和法沉降计算公式由公式（3）变形为：

公式中各参数意义详《建筑地基基础设计规范》GB 50007-2011附录R.0.4。

《建筑地基基础设计规范》GB 50007-2011第R.0.5条规定，采用明德林应力公式计算桩基础最终沉降量时，相应于作用的准永久组合时，轴心竖向力作用下单桩附加荷载的桩端阻力比α和桩基沉降计算经验系数ψpm应根据当地工程的实测资料统计确定。
无地区经验时，ψpm值可按表2选用。

明德林应力公式方法计算桩基沉降经验系数 表2

1936年，美国学者明德林(Raymond D.Mindlin) 在布辛奈斯克解的基础上推导出竖向荷载作用在弹性半无限体内部时体内任一点的应力与应变的数学解, 即明德林( Mindlin) 解。
工程实践表明：当用以计算深基础、桩长较长的桩基础沉降时，用明德林解分布求得的最终沉降与实测结果较为接近。
布辛奈斯克解与明德林解两者的区别在于，布辛奈斯克解所针对的应力应变关系都是在弹性半无限体的表面，而明德林解可以在弹性半无限体任何一点。

图4 竖向集中力作用于半无限体内部

如图4所示，竖向集中力P作用于半无限体内部某一深度c处，半无限弹性体内部M（x，y，z）点竖向附加应力σz的明德林解为：

式中：ν-土的泊松比。

由公式（5）可以看出，当c=0时，也就是荷载作用于地表时，公式（5）与公式（2）相同，明德林解退化为布辛奈斯克解，也就是说布辛奈斯克解仅仅是明德林解中荷载作用于弹性半无限体的表面的一个特例。

因此，对于天然基础或者桩长较短的桩基础，布辛奈斯克解与工程实际比较吻合；但是对于深基础或桩长较长的桩基础，明德林解更符合工程实际。

盖得斯（Geddes）根据桩的传递荷载特点，将轴心竖向力作用下单桩的附加荷载Q（相应于作用的准永久组合）分解为由桩端阻力Qp和桩侧摩阻力Qs共同承担，且Qp＝αQ，α是桩端阻力比；桩的端阻力假定为集中力，桩侧摩阻力可假定为沿桩身均匀分布和沿桩身线性增长分布两种形式组成，其值分别为βQ和(1-α-β)Q，如图5所示。
与此相应，盖得斯又根据明德林解，推导出桩端阻力Qp、均匀分布的桩侧摩阻力βQ、沿桩身线性增长的桩侧摩阻力(1-α-β)Q在地基土中产生的附加应力，进而计算出桩基的沉降。
这种方法称为明德林-盖得斯法，简称明德林法[4]。

图5 明德林-盖得斯单桩荷载分担

明德林（Raymond David Mindlin），1906年9月17日出生于美国纽约，1987年11月22日逝世，美国机械工程师（mechanical engineer）,哥伦比亚大学应用科学（Applied Science）教授。
1924年进入哥伦比亚大学，并获得文学、理学学士。
1933-1935年参加铁木辛柯（Stephen Prokofievitch Timoshenko）在密歇根大学任组织的夏季应用力学讨论会。
1936年将明德林解的论文发表在学术期刊《Physics》（现改为《Joumal of Applied Physics》）而获得哲学博士学位。

[1]《建筑地基基础设计规范理解与应用》编委会.建筑地基基础设计规范理解与应用（第二版）[M].北京：中国建筑工业出版社，2012.

[2]李广信,张丙印,于玉贞.土力学（第2版）[M].北京：清华大学出版社，2013.

[3]刘金波,李文平,刘民易,赵兵.建筑地基基础设计禁忌及实例[M].北京：中国建筑工业出版社，2013.

[4]周景星,李广信,张建红,虞石民,王洪瑾.基础工程（第3版）[M].北京：清华大学出版社，2015.