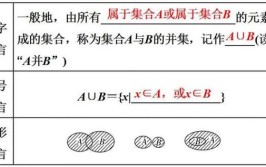
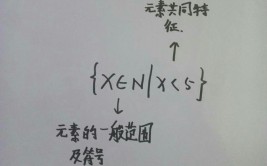
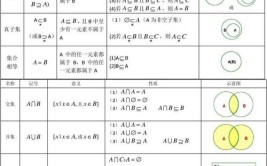
子集与真子集的区别是包含的范围不同。子集是一个集合中的全部元素是另一个集合中的元素,有可能与另一个集合相等。真子集是一个集合中的元素全部是另一个集合中的元素,但不存在相等。子集比真子集范围大,子集是包括本身元素的集合,真子集是除本身的元素的集合。
子集是一个数学概念:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。若∀a∈A,均有a∈B,则A⊆B。根据子集的定义,我们知道A⊆A。也就是说,任何一个集合是它本身的子集。
如果集合A是集合B的子集,并且集合B不是集合A的子集,那么集合A叫做集合B的真子集。如果A包含于B,且A不等于B,就说集合A是集合B的真子集。如果集合A⊆B,存在元素x∈B,且元素x不属于集合A,我们称集合A与集合B有真包含关系,集合A是集合B的真子集。记作A⫋B,读作“A真包含于B”。

(图片来自网络侵删)
集合在数学领域具有无可比拟的特殊重要性。集合论的基础是由德国数学家康托尔在19世纪70年代奠定的,经过一大批科学家半个世纪的努力,到20世纪20年代已确立了其在现代数学理论体系中的基础地位,可以说,现代数学各个分支的几乎所有成果都构筑在严格的集合理论上。